Abstract

A precision pendulum with two fixed axes, each having a period close to 1 s, has been outfitted with a small fully differential electronics package using a capacitive sensor. Power is received through the USB cable of the computer, which operates with a 24-bit analog to digital converter sampling the pendulum's motion at a frequency near 50 Hz. A user friendly software package provides real-time graphical display of the pendulum's free decay. Records stored in computer memory are available for later detailed investigation by a variety of analytic means.

Background

The heart of the instrument used for this study is the Kater pendulum sold commercially by Tel-Atomic Inc. [1], and which was described in a ``Physics Teacher'' article [2]. Apart from a research-oriented activity [3], it has only been previously monitored with timers used to measure its period.

Typically the earth's gravitational field is measured with a pendulum using only a stopwatch (manually) or a period counter (electronically). Although the latter is more accurate than the former, both methods are primitive as compared to the results that can be achieved with a sensor that monitors full motion of the pendulum [4]. Such a sensor was used for the study [3]; however, the electronics employed for that work is of a type that is no longer commercially available. The NE5521n chip that was the key component used in conjunction with the fully differential capacitive sensor [5] ceased to be readily available after a factory fire. Fortunately, not long afterwards, Analog Devices marketed its capacitance to digital converter (AD7745), which is used in the sensor package of the present work. It is also employed in the computerized Cavendish balance [6], another instrument that was designed by the first author of the present article. Its use of two capacitive sensors to monitor boom motion allows for a `mechanical common mode rejection' that makes it more user-friendly than traditional Cavendish experiments based on optical sensing.

Instrument

Shown in Fig. 1 is a photograph of the brass bar pendulum.

Figure 1. Rotation axes are provided by hanging the bar on a `knife edge' that is visible in Fig. 2. For `end axis' oscillation, the hole close to the end of the bar is used. For `mid axis' oscillation, the other hole is employed. The bar was computer-designed to yield an approximate 1 s period for each of the two axes.

Figure 2 shows the pendulum configured to swing about the end-axis.

Figure 2. Seen mounted on the pendulum is a small square nylon mass whose position on the pendulum is adjustable. This sliding mass is used in the method for estimating `little g' most accurately, and which is described later in detail, in the context of some representative data.

Estimates of g (approx 9.8 m/s²) require that data be collected using both axes. For operation about the mid axis, the clamp seen near the top of the Fig. 2 picture would be repositioned on the vertical steel rod. It would be a lower clamped position for which the end hole is made to swing along an arc that is below the position of the active elements of the capacitive sensor electrodes. The electrodes are not visible, since their pc boards have been wrapped with heat shrinkable plastic to avoid any shorting of the electronics that might happen if the brass pendulum should come into contact with them through misalignment. The whole electronics package is pictured in more detail in Fig. 3.

Figure 3. Closeup photograph of the electronics. The top clamp is positioned for a clearance of about half a cm between the bar end and the bottom plastic piece sitting on top of the aluminum box that houses the electronics.

Representative data obtainable with the pendulum

The package is readily configured to operate with any of the most common computer systems, whether Windows or Linux software, and hardware that is either 32-bit or 64-bit. Data of the present article were obtained with an XP laptop operating with a 32-bit cpu.

Shown in Fig. 4 are some long-term free-decays involving oscillation about both axes.

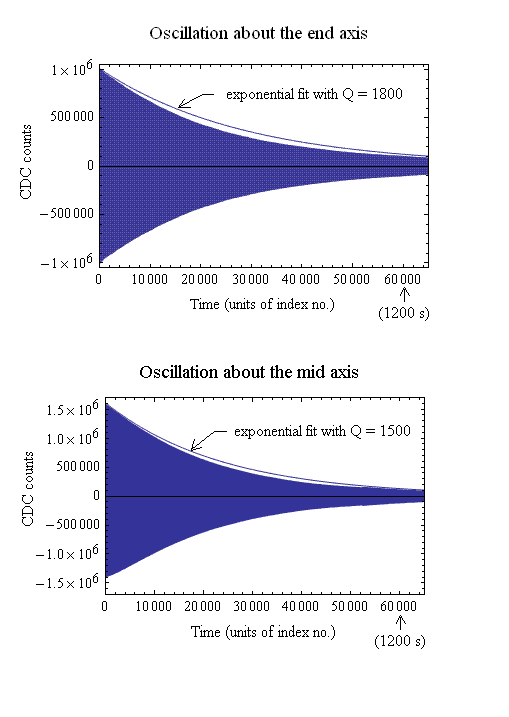
Figure 4. Free-decays showing exponential fits to the positive turning points. The fits were computed with Excel, but the total number of points at 60,000 is too large for graphing with Excel. The graphs were generated using Mathematica.

To obtain a given free decay the pendulum was set into motion manually, by pushing on the bar with a finger resting on top of the sensor electrodes. It is seen from Fig. 4 that energy dissipation of the pendulum is more complicated than simple viscous damping. The Reynolds number is initially large enough for air drag to involve a quadratic term in the velocity. Thus, except at the start and end points, it causes the record to dip below the exponential. The deviation is seen to be greater for end axis oscillation than for mid axis oscillation. The quality factors also differ, being larger at 1800 for the former and 1500 for the latter. These numbers are only approximate, since Q is amplitude dependent except for viscous damping [7].

Textbooks routinely give the impression that a damping correction must be generally applied to an estimate for the period of a mechanical oscillator. In other words, when the equation of motion is of the form

involving a viscous (linear) damping parameter b, the period of oscillation is given by

It is difficult to experimentally verify the damping redshift predicted theoretically by this equation. As seen from the following log-log graph, it amounts to less than one part in 10 million for the present experiments, where Q > 1000.

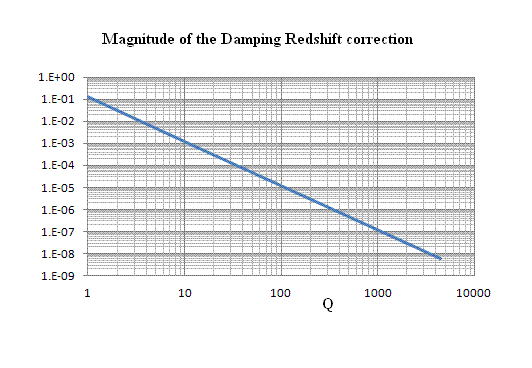
Figure 5. Fractional value of the damping redshift|(f - f₀)/f₀| plotted as a function of the quality factor.

For efforts to estimate the earth's field to one part in ten thousand, there is clearly no need to worry about the complications of Eq.(2).

Measurement Technique

As with the technique used in ref. 4, we here choose to work with Lissajous figures, and two examples are provided in Fig. 6.

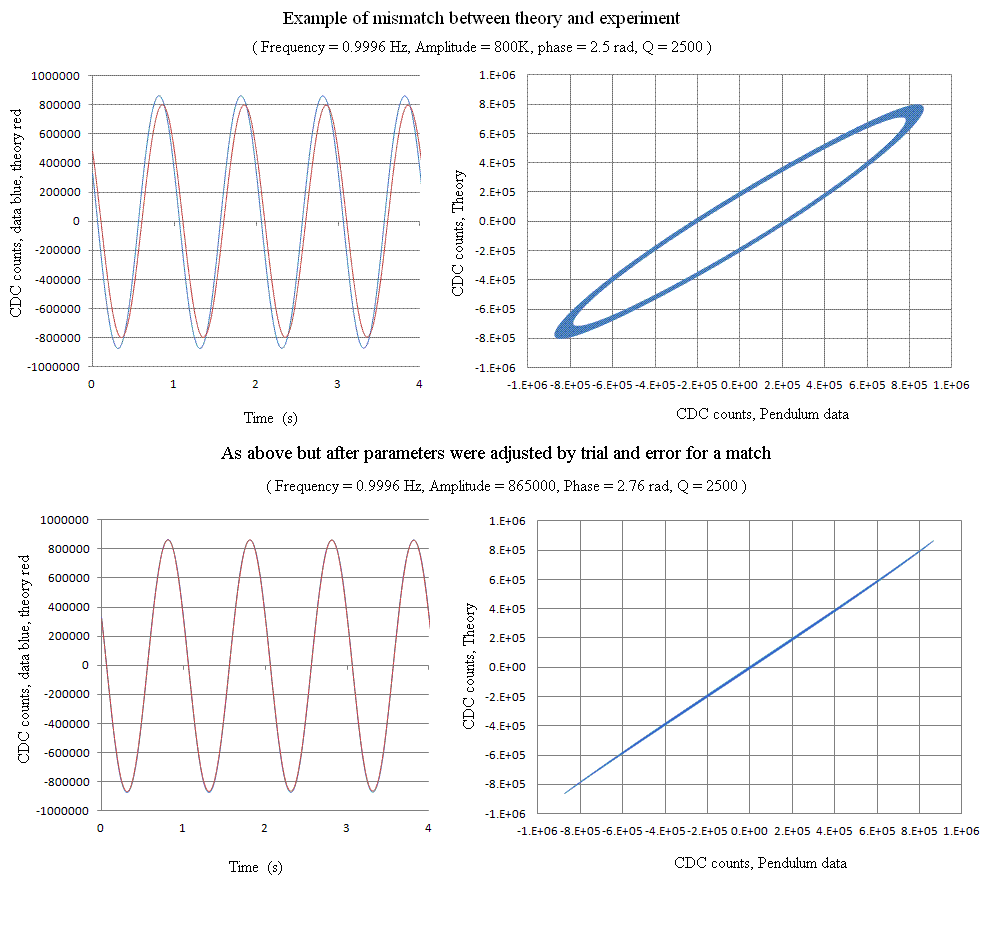
Figure 6. Illustration of the method used to obtain a theoretical fit to the data. Only 4 seconds are shown in the time plots, of the 88 s total time recorded. All 4400 points were included in the generation of the Lissajous figures.

The frequency measurement is determined by the sample rate of the electronics, which was measured to be 49.93 Hz. Although this number of acquired samples per second is somewhat variable and temperature dependent, a change of about 50 Celsius degrees is required for an increase in the frequency of one part per thousand. Based on the authors' experience with the package, it is expected that the oscillator in the electronics that is responsible for this sample rate should be stable to a few parts per ten thousand for the typical laboratory environment.

For accurate estimates of g the frequency needs to be checked carefully the first time and maybe periodically thereafter. It is readily done using a quartz-based stopwatch or by comparison with the NIST standard wwv. An equivalent to the latter (radio broadcast signal) can be monitored via the internet. By comparing the two for a total time of 5 to 10 minutes, the sample rate can be measured to a part per ten thosand; the objective sought in estimates of the earth's field when measured with this Kater pendulum.

The beauty of the Kater method is the following. If the periods about the two axes can be matched, then the instrument is equivalent to a simple pendulum whose length equals the distance between the axes; which for the Tel-Atomic unit is 0.2481 m. If they are `slightly' different, then the following equation can be used to estimate g in m/s² typically to a few parts per thousand:

To thus use Eq.(3) the mid axis oscillation that was recorded yielded the graphs of Fig. 7.

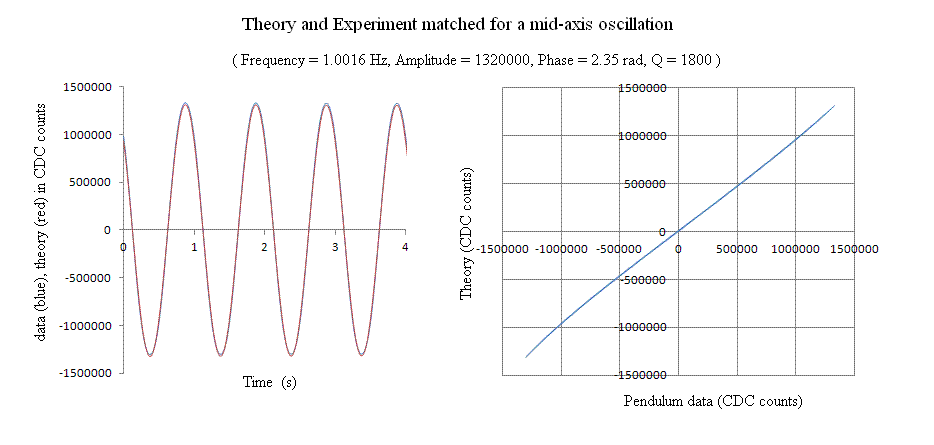
Figure 7. As with the bottom set of Fig. 6 but oscillating about the mid axis. The estimated frequency for this case (based on the theoretical parameter yielding a match) was 1.0016 Hz.

Based on the frequencies indicated in Figures 6 and 7, one obtains from Eq.(3) an estimate of g  =  9.77 m/s². We will see from the data presented later, obtained with a small mass slider whose position on the bar is adjustable-that for differences as small as typically encountered with the Tel-Atomic Kater pendulum-a better estimate for g is possible. It is obtained by using g  =  4 pi² L (T_mid/T_end³ + 1/ T_mean²)/2, where L = 0.2481 m and T_mean  =  (T_end + T_mid)/2. For the values indicated in Figures 6 and 7, this yields g  =  9.787 m/s²; which differs by one part per thousand from the value of 9.797 that was obtained in a previous careful measurement of the earth's field in Macon, Ga [2].

Use of the sliding mass

As described in [2], the most accurate means for estimating g is to measure the period of each of the two axes as a function of the position of the slider that is pictured in Fig. 1. By means of a center punch during fabrication, a set of 35 small-point indentations span the brass bar through nearly its entire length. Beginning farthest from the end axis, these markers spaced in 1 cm intervals would number 36, except that the mid axis hole disallows the use of marker number 13.

For the present work, slider positions 8 through 17 were employed, yielding the graph shown in Fig. 8.

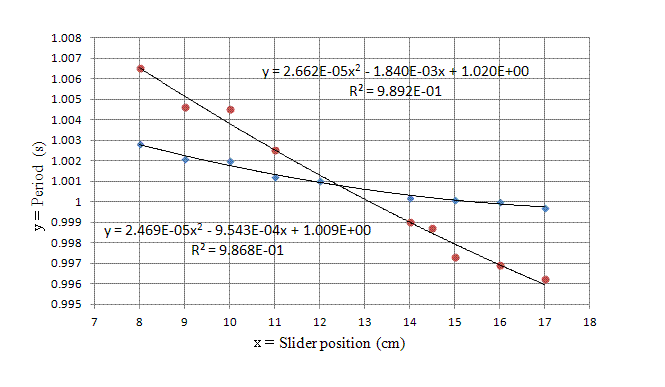
Figure 8. Data used in estimating g with the highest accuracy. End axis periods are represented by the blue diamonds and mid axis periods by the red circles.

Each of the 18 period measurements performed for the generation of this figure used a Lissajous figure generated by Excel, in which the pendulum was monitored for a total decay time of 10 s. Using the quadratic trendline fit expressions indicated in Fig. 8, Excel was used to find the period corresponding to the intersection of the two curves. This period of 1.0007 s yields an estimate for g of 9.801 m/s², which differs from the Macon `standard' by 5 parts per ten thousand. It is expected that the difference would become smaller as more points should be used in the generation of Fig. 8.

Precision of the Lissajous measurement

As demonstrated in Fig. 9, the Lissajous technique is amenable to a parts per ten thousand match of a theoretical fit to a record whose total length is 10 s.

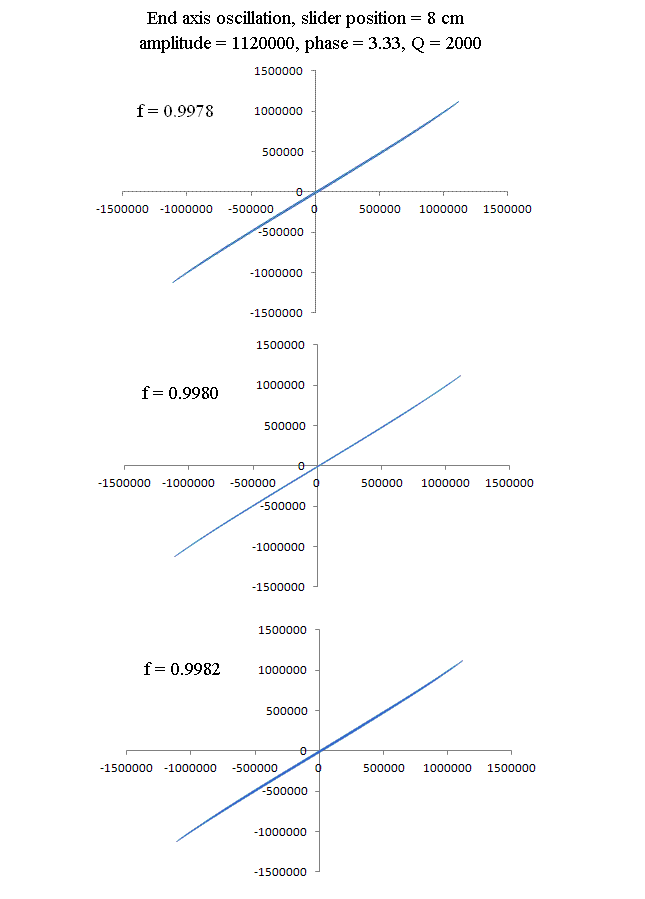
Figure 9. Representative example to illustration sensitivity to choice for the theoretical value of pendulum frequency. Record length in all three cases was the same 10 s, and all the indicated fit parameters were held constant except for the frequency,.

It can be seen from Fig. 9 that `thickening' of the Lissajous `line' becomes detectable if the frequency deviates from the best fit value by more than two parts per ten thousand.

Use of Excel to generate the Lissajous figures

Excel can be readily configured with a template to rapidly generate the Lissajous figures. Parameter adjustments by trial and error, that influence the graph almost instantaneously, are configured for updates using `absolute' referencing. A given raw data set is input to the template by means of paste operations using hot keys. Selection of the Q is of least importance, followed by choice of the amplitude parameter. These are selected most readily by also graphing a time display of theory and experiment on the same plot. A rough setting of phase and frequency are then also performed using the time plot. Once a reasonably narrow line has been realized for the Lissajous curve, it is then the only graph considered in the final selection for values of the phase and frequency parameters. The technique used is similar to that of finding the root of a function by jumping back and forth either side of the solution, with ever smaller deviations from one choice to the next.

As noted earlier, the `best' estimate for a rapid determination of g, using the Tel-Atomic Kater pendulum, is evidently the one which uses an average involving (i) Eq. (8), and (ii) the mean value of the periods obtained from the mid and end axes. The evidence for this claim is found in Fig. 10.

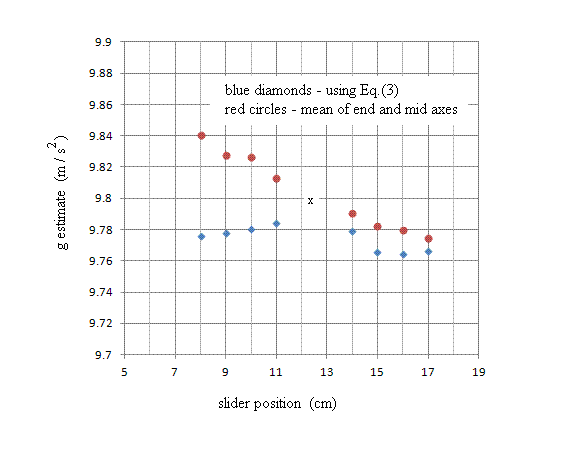
Figure 10. Comparison of g estimates based on two different methods, with calculations using the same period values as the data graphed in Fig. 8. An x has been placed at the position corresponding to identical periods of end axis and mid axix.

Over the full range of slider position from 8 to 17 cm, the method of Eq.(3) is seen (in a global average sense) to provide a generally better estimate for g than the method which works simply with the mean period of the two axes. For a Kater pendulum with nearly matched periods the simple mean method evidently gives comparable accuracy to the method using Eq.(3). Because of the cusp in the plot of the latter, it is seen that the best approach is to use the avereage of the two methods.

Noise level of the electronics

Because of the fully differential electronics, and the 24 bit adc electronics package (21 bits employed in record saves), the signal to noise ratio of measurements performed with this instrument is remarkably great. Its magnitude is readily appreciated by comparing Fig. (7) with the next Fig. (11), which was obtained after placing the pendulum on the pier of the seismic station in the Mercer Physics department.

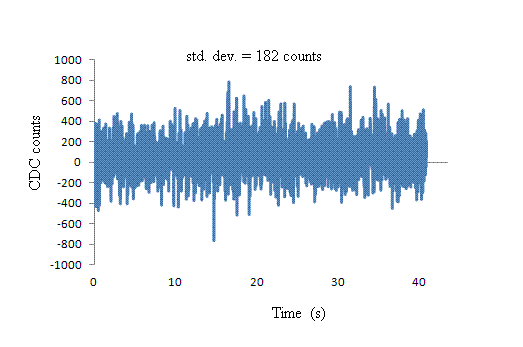
Figure 11. Electronics noise measured by placing the pendulum on a seismic pier and providing a cover to eliminate air current disturbances.

For a max-amplitude value of 1,300,000 CDC counts and a noise floor of 182 CDC counts, we find an operational SNR > 7000.

Sensor Linearity

It is also noteworthy that the linearity of the sensor is excellent, as can be seen from Fig. 12.

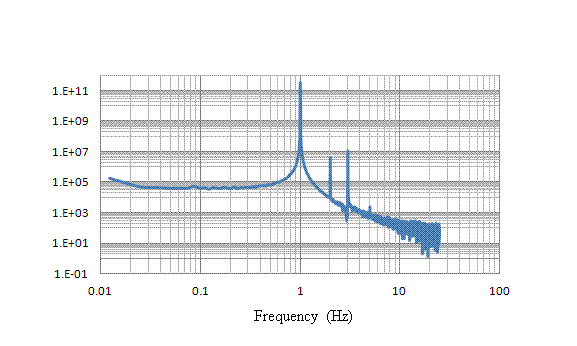
Figure 12. 4096-point FFT spectrum of an 88 s duration record obtained using end axis oscillation. The amplitude of the motion was 865,000 CDC counts.

The pendulum's natural frequency is seen as the prominent spectral line at 1 Hz, and two of its harmonics are visible in the log-log plot. Harmonic distortion is very low at -49 dB for the 2nd harmonic and -45 dB for the 3rd harmonic.

References

[1] described online at http://telatomic.com/mechanics/kater_pendulum.html

[2] R. D. Peters, ``Student-friendly precison pendulum'', The Physics Teacher, 37, Issue 7, p. 390 (1999).

[3] R. D. Peters, ``Study of simple harmonic oscillator resonance using a compact Kater pendulum'', online at http://physics.mercer.edu/hpage/kater-res.html

[4] R. D. Peters, ``Automated Kater Pendulum'', Eur. J. Phys. 18 (1997) 217-221. Online at http://iopscience.iop.org/0143-0807/18/3/016/pdf/0143-0807_18_3_016.pdf

[5]``Symmetric differential capacitance transducer employing cross coupled conductive plates to form equipotential pairs'', U. S. Patent 5,461,319. The predecessor LRDC sensor, also invented by Peters, was the first version of ``fully differential capacitive sensors'', which are becoming increasingly commonplace in engineering applications.

[6] described online at http://telatomic.com/mechanics/cavendish_balance.html

[7] The amplitude dependence of Q for nonlinear damping is treated on page 20-52 of:
R. D. Peters, ``Damping Theory'', Vibration and Shock Handbook, CRC Press, ed. Clarence W. de Silva (2005). The same material is also available in Ch. 2 of Vibration Damping, Control and Design, CRC Press, (2007).